В отличие от аналоговых электронных устройств, в цифровых устройствах (ЦУ) входные и выходные сигналы могут принимать ограниченное количество состояний. В соответствии с логическим соглашением (ГОСТ 2.743-82), в зависимости от конкретной физической реализации элементов ЦУ, более положительному значению физической величины, "H" - уровень, соответствует состояние "логическая 1", а менее положительному значению,"L - уровень" - "логический 0". Такое соглашение называется положительной логикой. Обратное соотношение называется отрицательной логикой. В ГОСТе 19480 - 89 даны наименования, определения и условные обозначения основных параметров и характеристик цифровых микросхем.
Теоретической основой проектирования ЦУ является алгебра-логики или булева алгебра, оперирующая логическими переменными. Для логических переменных, принимающих только два значения, существуют 4 основных операции. Операция логическое "И" (AND) конъюнкция или логическое умножение, обозначается * или /\. Операция логическое "ИЛИ" (OR), дизъюнкция или логическое сложение, обозначается + или \/. Операция логическое "НЕ" (NOT), изменение значения, инверсия или отрицание, обозначается чертой над логическим выражением. Инверсия иногда будет в тексте обозначаться знаком "~". Операция эквивалентности обозначается "=".
Высказывание (суждение) – некоторое предложение, которое может быть истинно (верно) или ложно
Утверждение – суждение, которое требуется доказать или опровергнуть
Рассуждение – цепочка высказываний или утверждений, определенным образом связанных друг с другом
Умозаключение – логическая операция, в результате которой из одного или нескольких данных суждений получается (выводится) новое суждение
Логическое выражение – запись или устное утверждение, в которое, наряду с постоянными, обязательно входят переменные величины (объекты). В зависимости от значений этих переменных логическое выражение может принимать одно из двух возможных значений: ИСТИНА (логическая 1) или ЛОЖЬ (логический 0)
Сложное логическое выражение – логическое выражение, составленное из одного или нескольких простых (или сложных) логических выражений, связанных с помощью логических операций.
Логические операции и таблицы истинности
F = A & B
 Логическое умножение КОНЪЮНКЦИЯ - это новое сложное выражение будет истинным только тогда, когда истинны оба исходных простых выражения. Конъюнкция определяет соединение двух логических выражений с помощью союза И.
Логическое умножение КОНЪЮНКЦИЯ - это новое сложное выражение будет истинным только тогда, когда истинны оба исходных простых выражения. Конъюнкция определяет соединение двух логических выражений с помощью союза И.
F = A + B

Логическое сложение ДИЗЪЮНКЦИЯ - это новое сложное выражение будет истинным тогда и только тогда, когда истинно хотя бы одно из исходных (простых) выражений. Дизъюнкция определяет соединение двух логических выражений с помощью союза ИЛИ.
 Логическое отрицание ИНВЕРСИЯ - если исходное выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное выражение ложно, то результат отрицания будет истинным. Данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.
Логическое отрицание ИНВЕРСИЯ - если исходное выражение истинно, то результат отрицания будет ложным, и наоборот, если исходное выражение ложно, то результат отрицания будет истинным. Данная операция означает, что к исходному логическому выражению добавляется частица НЕ или слова НЕВЕРНО, ЧТО.

Логическое следование ИМПЛИКАЦИЯ - связывает два простых логических выражения, из которых первое является условием (А), а второе (В)– следствием из этого условия. Результатом ИМПЛИКАЦИИ является ЛОЖЬ только тогда, когда условие А истинно, а следствие В ложно. Обозначается символом "следовательно" и выражается словами ЕСЛИ …, ТО …

Логическая равнозначность ЭКВИВАЛЕНТ-НОСТЬ - определяет результат сравнения двух простых логических выражений А и В. Результатом ЭКВИВАЛЕНТНОСТИ является новое логическое выражение, которое будет истинным тогда и только тогда, когда оба исходных выражения одновременно истинны или ложны. Обозначается символом "эквивалентности".
Порядок выполнения логических операций в сложном логическом выражении:
1. Инверсия;
2. Конъюнкция;
3. Дизъюнкция;
4. Импликация;
5. Эквивалентность.
Для изменения указанного порядка выполнения операций используются скобки.
Построение таблиц истинности для сложных выражений:
Количество строк = 2n + две строки для заголовка (n - количество простых высказываний)
Количество столбцов = количество переменных + количество логических операций
При построении таблицы надо учитывать все возможные сочетания логических значений 0 и 1 исходных выражений. Затем – определить порядок действий и составить таблицу с учетом таблиц истинности основных логических операций.
ПРИМЕР: составить таблицу истинности сложного логического выражения D = не A & (B+C) (таблица 3).
А, В, С - три простых высказывания, поэтому:
- количество строк = 23 +2 = 10 (n=3, т.к. на входе три элеманта А, В, С)
- количество столбцов: 1) А; 2) В; 3) С; 4) не A это инверсия А (обозначим Е); 5) B + C это операция дизъюнкции (обозначим F); 6) D = не A & ( B+C ), т.е. D = E & F это операция конъюнкции.
Таблица 3 - таблица истинности логического выражения D = не A & (B+C)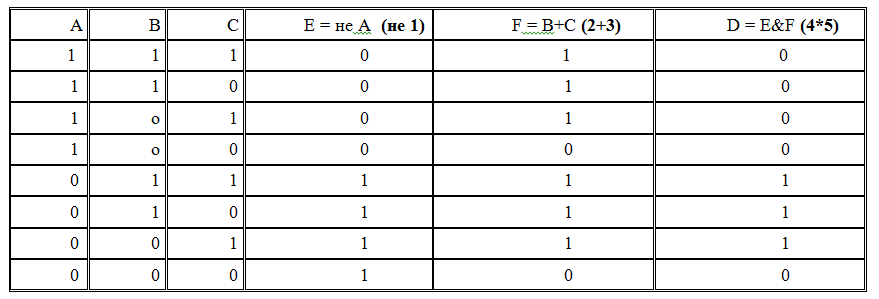

| < Предыдущая | Следующая > |
|---|







