Математическая логика имеет непосредственную связь с теорией проектирования ЭВМ. С помощью логических функций и законов математической логики может быть описано поведение различных компонентов ЭВМ. Кроме того, современные языки программирования немыслимы без встроенных в них логических функций.
При записи тех или иных логических выражений используется специальный язык, который принят в математической логике. Ее основоположником является великий немецкий математик Готфрид Вильгельм Лейбниц. Ирландский математик Джордж Буль продолжил создание математической логики, которая оперирует не числами, а высказываниями. Высказывание - это любое утверждение, относительно которого можно сказать: истинно оно или ложно.
Так, например, предложение “7 - нечетное число” следует считать высказыванием, так как оно истинное. Предложение “Июль - зимний месяц” тоже высказывание, так как оно ложное.
Разумеется, не всякое предложение является логическим высказыванием. Высказываниями не являются, например, предложения “ученик десятого класса” и “информатика - интересный предмет”. Первое предложение ничего не утверждает об ученике, а второе использует слишком неопределённое понятие “интересный предмет”. Вопросительные и восклицательные предложения также не являются высказываниями, поскольку говорить об их истинности или ложности не имеет смысла.
Предложения типа “в городе A более миллиона жителей”, “у него голубые глаза” не являются высказываниями, так как для выяснения их истинности или ложности нужны дополнительные сведения: о каком конкретно городе или человеке идет речь. Такие предложения называются высказывательными формами.
Высказывательная форма - это повествовательное предложение, которое прямо или косвенно содержит хотя бы одну переменную и становится высказыванием, когда все переменные замещаются своими значениями.
Употребляемые в обычной речи связки: "не”, “и”, “или”, “если... , то”, “тогда и только тогда” и другие позволяют из уже заданных высказываний строить новые. Такие слова и словосочетания называются логическими связками.
Высказывания, образованные из других высказываний с помощью логических связок, называются составными. Высказывания, не являющиеся составными, называются элементарными.
Элементарные высказывания соответствуют алгебраическим переменным, составные – функциям.
Так, например, из элементарных высказываний “Иванов - сыщик”, “Иванов - скрипач” при помощи связки “и” можно получить составное высказывание “Иванов - сыщик и скрипач”, понимаемое как “Иванов - сыщик, хорошо играющий на скрипке”.
При помощи связки “или” из этих же высказываний можно получить составное высказывание “Иванов - сыщик или скрипач”, понимаемое в алгебре логики как “Иванов или сыщик, или скрипач, или и сыщик и скрипач одновременно”.
Истинность или ложность получаемых таким образом составных высказываний зависит от истинности или ложности элементарных высказываний.
К основным логическим операциям относят операцию НЕ (отрицание, инверсия – NOT), операцию И (логическое умножение, конъюнкция – AND), операцию ИЛИ (логическое сложение, дизъюнкция – OR).
В математической логике определяется специальная алгебра – алгебра логики, содержащая операции конъюнкции, дизъюнкции и отрицания, которые позволят производить тождественные преобразования логических выражений.
В отличие от обычной алгебры, изучающей математические функции, алгебра логики изучает логические функции. Известно, что функция – это закон соответствия между переменными. Следовательно, логическая функция – это закон соответствия между логическими переменными. Логическая переменная – это такая переменная, которая может принимать одно из двух возможных значений: 0 («ложь») и 1 («истина»). Логическая функция может также принимать два значения. Из этого следует, что логические переменные и функции определены на множестве двух значений – {0,1}.
Логические функции характеризуются (задаются) так называемыми таблицами истинности, или соответствия. Таблица истинности представляет собой таблицу, устанавливающую соответствие между возможными значениями наборов переменных и значениями функции. Сложные логические функции, как правило, выражаются через простые. Простые логические функции, зависящие от одной или двух логических переменных, называются элементарными. Ниже приведены таблицы истинности базовых логических операций.
Таблица - Основные логические операции

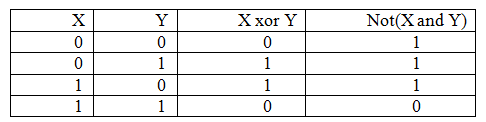
В вычислительной технике также часто используется операция «исключающее ИЛИ» (XOR), которая фактически сравнивает на совпадение два двоичных разряда. На практике, по технологическим причинам в качестве основного логического элемента используется элемент И-НЕ.
Таблица - Дополнительные логические операции
ЭВМ строятся из компонентов с двумя устойчивыми состояниями. Одно состояние обозначается нулем, другое – единицей. На такие компоненты воздействуют двоичные сигналы. Под воздействием сигналов компоненты изменяют свои состояния, т.е. состояние компонентов или значения их выходных сигналов зависят от значений воздействующих сигналов. Очевидно, что функционирование компонентов ЭВМ следует описывать логическими функциями. По этой причине алгебра логики находит непосредственное и широкое применение при разработке и использовании средств электронной вычислительной техники.
Математический аппарат алгебры логики очень удобен для описания функционирования аппаратных средств компьютера, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже два: “1” и “0”.
Из этого следует два вывода:
1. Одни и те же устройства компьютера могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных.
2. На этапе конструирования аппаратных средств алгебра логики позволяет значительно упростить логические функции, описывающие функционирование схем компьютера, и, следовательно, уменьшить число элементарных логических элементов, из десятков тысяч которых состоят основные узлы компьютера.
Обработка информации в ЭВМ происходит путем последовательного выполнения элементарных операций. К ним относятся: установка, сдвиг, прием, преобразование, сложение и некоторые другие. Для выполнения каждой из этих операций сконструированы электронные узлы – регистры, счетчики, сумматоры, преобразователи кодов и т.д. Из этих узлов строятся интегральные микросхемы очень высокого уровня: микропроцессоры, модули ОЗУ, контроллеры внешних устройств и т.д. Сами указанные узлы собираются из основных базовых логических элементов – как простейших, реализующих логические функции И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и им подобных, так и более сложных, таких как триггеры.
Логический элемент компьютера - это часть электронной логической схемы, которая реализует элементарную логическую функцию.
Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем.
Введем условные обозначения основных логических элементов.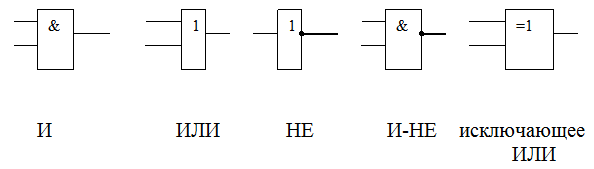
Данные простейшие логические элементы можно реализовать аппаратно. Это означает, что можно создать электронные устройства на транзисторах, резисторах и т.д., каждое из которых имеет один или два входа для подачи управляющих напряжений и один выход, напряжение на котором определяется соответствующей таблицей истинности. На практике логическому «да» соответствует наличие напряжения, логическому «нет» - его отсутствие.
В качестве характерных устройств выберем два наиболее важных и интересных – триггер и сумматор. Триггер – это электронная схема, широко применяемая в регистрах компьютера для надёжного запоминания одного разряда двоичного кода. Сумматор - это электронная логическая схема, выполняющая суммирование двоичных чисел.
Простейший вариант триггера собирается из четырех логических элементов И-НЕ (рисунок 13). Он имеет два входа R, S и два выхода – прямой и инверсный . Термин триггер происходит от английского слова trigger - защёлка, спусковой крючок. Для обозначения этой схемы в английском языке чаще употребляется термин flip-flop, что в переводе означает “хлопанье”. Это звукоподражательное название электронной схемы указывает на её способность почти мгновенно переходить (“перебрасываться”) из одного электрического состояния в другое и наоборот.
Самый распространённый тип триггера - так называемый RS-триггер (S и R, соответственно, от английских set - установка, и reset -сброс).

Логическая схема триггера
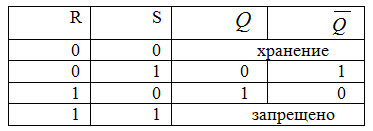
Проанализируем возможные комбинации значений входов R и S триггера, используя его схему и таблицу истинности схемы И-НЕ.
1. Пусть на входе R установлена 1, а на входе S – 0. Логические элементы D1 и D2 инвертируют эти сигналы. В результате на вход элемента D3 поступает 1, а на D4 – 0. Поскольку на одном из выходов D4 уже есть 0, независимо от состояния другого входа на его выходе (он же инверсный выход триггера) обязательно установится 1. Эта 1 передается на вход элемента D3 и в сочетании с 1 на другом входе порождает на выходе D3 логический 0. Итак, при R=1 и S=0 на прямом выходе триггера устанавливается 0, а а на инверсном – 1. Обозначение состояния триггера принято связывать с прямым выходом: говорят, что триггер «устанавливается в 0» или «сбрасывается». Отсюда и вход, появление сигнала на котором приводит к сбросу триггера обозначают, R (“reset”).
2. При аналогичных рассуждениях для симметричного случая R=0 и S=1, можно убедиться, что триггер перейдет в единичное состояние – «установится» (“set”).
3. Наиболее распространенная и интересная ситуация, когда R=0 и S=0 – входные сигналы сняты. Состояние выхода будет полностью зависеть от состояния противоположных входов. Такое состояние будет устойчивым: 0 на одном из выходов будет поддерживать 1 на другом. Таким образом, при отсутствии входных сигналов триггер будет сохранять свое «предыдущее» состояние. Это свойство триггера и положено в основу хранения одного бита информации.
4. Последняя комбинация R=1 и S=1 приводит к тому, что на обоих выходах триггера установиться 1! Такое состояние логически недопустимо и крайне неустойчиво, поскольку снятие входных напряжений приведет к тому, что триггер случайным образом перейдет в одно из своих устойчивых состояний. Такая ситуация на практике является запрещенной. Ниже приведена таблица истинности триггера.
Поскольку один триггер может запомнить только один разряд двоичного кода, то для запоминания байта нужно 8 триггеров, для запоминания килобайта, соответственно, 8 * 210 = 8192 триггеров. Современные микросхемы памяти содержат миллионы триггеров.
Таблица истинности RS-триггера
Сумматор - это электронная логическая схема, выполняющая суммирование двоичных чисел.
Сумматор служит, прежде всего, центральным узлом арифметико-логического устройства компьютера, однако он находит применение также и в других устройствах машины.
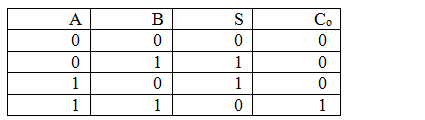
Многоразрядный двоичный сумматор, предназначенный для сложения многоразрядных двоичных чисел, представляет собой комбинацию одноразрядных сумматоров. Начнем с изучения логической структуры простейшего возможного устройства, являющегося звеном сумматора – полусумматора, который реализует сложение двух одноразрядных двоичных чисел. В результате получается двухразрядное двоичное число. Его младшую цифру обозначим S, а старшую, которая при сложении многоразрядных чисел будет перенесена в старший разряд, через Co (от английских слов “Carry out” – “выходной перенос”).
Обе цифры можно получить по следующим логическим формулам:
![]()
Составим для этих формул таблицу истинности.
Таблица истинности для полусумматора
Таким образом, для реализации полусумматора достаточно соединить параллельно входы двух логических элементов, как это показано на рисунке.

Логическая схема полусумматора
Полный одноразрядный сумматор при сложении двух цифр может учитывать возможное наличие единицы, переносимой из старшего разряда. Обозначим этот «бит переноса» через Ci (от английского «Carry in» - «входной перенос»).
При построении схемы сумматор (рис.) удобно представить в виде двух полусумматоров, из которых первый суммирует разряды числа, а второй к полученному результату прибавляет бит переноса. Ниже приводится таблица истинности одноразрядного сумматора.
Таблица. Таблица истинности для одноразрядного сумматора
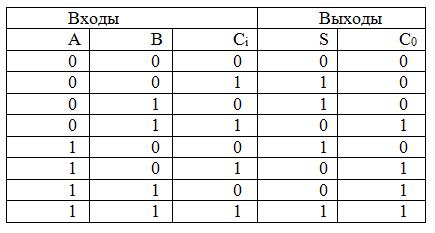
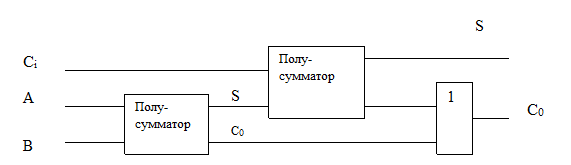
Сумматор, составленный из двух полусумматоров
Перейти к многоразрядным числам можно путем последовательного соединения соответствующего количества сумматоров.
Данная последовательность логических схем отражает важнейшую в современной цифровой электронике и вычислительной технике идею последовательной интеграции. Такая интеграция позволяет реализовать все наиболее функционально сложные узлы современного компьютера.
| < Предыдущая | Следующая > |
|---|







