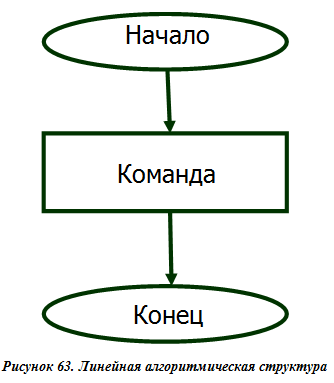
Линейная алгоритмическая структура
Существует большое количество алгоритмов, в которых команды должны быть выполнены последовательно одна за другой. Такие последовательности команд будем называть сериями, а алгоритмы, состоящие из таких серий, линейными.
Линейный алгоритм заключается в том, что шаги алгоритма следуют один за другим не повторяясь, действия происходят только в одной заранее намеченной последовательности.
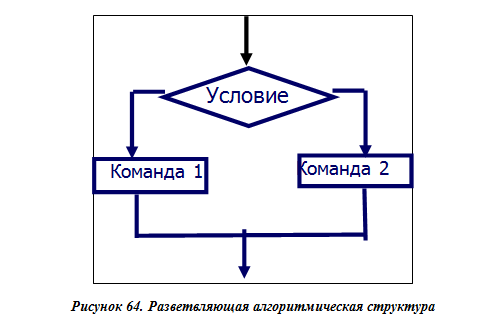
Разветвляющая алгоритмическая структура
В алгоритмическую структуру «ветвление» входит условие, в зависимости от выполнения или невыполнения которого реализуется та или иная последовательность команд. Алгоритм с ветвлением означает, что в зависимости от выполнения или невыполнения условия исполняется либо одна, либо другая ветвь алгоритма. Условие – высказывание, которое может быть либо истинным, либо ложным. Условие, записанное на формальном языке, называется условным, или логическим выражением. Условные выражения могут быть простыми и сложными. Простое условие включает в себя два числа, две переменных или два арифметических выражения, которые сравниваются между собой с использованием операций сравнения (равно, больше, меньше). Например, 5 > 3, 2 * 8 = 4 * 4. Сложное условие – это последовательность простых условий, объединенных между собой знаками логических операций. Например, 5 > 3 And 2 * 8 = 4 * 4.
Типовые алгоритмы можно подразделить на алгоритмы обработки массивов, алгоритмы поиска и алгоритмы сортировки.
Типовые алгоритмы обработки массивов:
1. Суммирование двух массивов одинакового размера
Задано: массивы A = (a1, a2, ..., an), B = (b1,b2,...,bn).
Сформировать: массив C =(c1, c2, ..., cn), где Сi = Ai + Bi; i = 1, 2, ..., n.
Задача сводится к организации цикла по i и вычислению Ci = Ai + Bi при каждом значении i от 1 до n.
Исходные данные:
N - размер массива;
A, B - массивы слагаемые размером N;
Результат: массив С - размером N;
Вспомогательные переменные: I - индекс - управляющая переменная цикла.
Procedure SUM_MAS (n : integer; A,B :mas; var C : mas);
{ где mas должен быть описан в главной программе в разделе описания типов, например так:
type mas = array[1..100 ] of real ;
тогда это будет процедура для суммирования двух одномерных массивов размером не более 100 элементов }
begin
for i := 1 to n do C[i] := A[i]+B[i];
end.
2. Суммирование элементов массива.
Задано: массив P = (P1,P2,...,Pn).
Определить: сумму элементов массива.
Исходные данные:
N - размер массива;
P - массив размером N;
Результат: S - сумма элементов;
Вспомогательная переменная: I - индекс - управляющая переменная цикла.
Procedure SUMMA (n : integer; A :mas; var S : real );
{ процедура для суммирования элементов одномерного массива }
begin S:=0; { обнуление переменной под сумму }
for i := 1 to n do S := S+P[i]
end.
3. Определение числа элементов массива, удовлетворяющих заданному условию.
Задано: массив P = (P1,P2,...,Pn); T - заданное число.
Определить: сколько элементов удовлетворяет заданному условию, например Pi > T.
Исходные данные:
N - размер массива;
P - массив размером N;
T - заданное значение, с которым сравниваются элементы массива.
Результат: K - число элементов массива P, удовлетворяющих условию.
Вспомогательная переменная: I- индекс - управляющая переменная цикла.
Procedure USLOVIE ( n : integer; P :mas; T: real; var K : integer);
{процедура определения числа элементов, удовлетворяющих условию}
begin
k := 0; { обнуление переменной под счетчик чисел }
for i := 1 to n do if P[ i ] > T then k := k+1
end;
4. Суммирование элементов массива, удовлетворяющих заданному условию.
Задано: массив P = (P1,P2,...,Pn); T - заданное число.
Определить: сумму элементов массива P, удовлетворяющих заданному условию, например Pi > T.
Исходные данные:
N - размер массива;
P - массив размером N;
T - заданное значение, с которым сравниваются элементы массива;
Результат: S - сумма элементов массива P, удовлетворяющих условию.
Вспомогательная переменная : I - индекс - управляющая переменная цикла.
Procedure SUM_USLOV ( n : integer; P :mas; T: real; var S : real);
{процедура определения суммы элементов, удовлетворяющих условию}
begin S := 0; {обнуление переменной под сумму элементов}
for i := 1 to n do if P [ i ] > T then S := S+1
end;
Задано: массив C = (c1,c2,...,cn).
Требуется: изменить порядок следования элементов массива C на обратный, используя одну вспомогательную переменную.
Исходные данные:
N - размер массива;
C - массив размером N;
Результат:
C - инвертированный массив;
Вспомогательные переменные:
I -индекс, управляющая переменная цикла;
M = n/2 - вычисляется до входа в цикл для уменьшения объема вычислений; P - используется при перестановке двух элементов массива.
Procedure INVER_MAS ( n : integer; C :mas; var C : mas);
Var m : integer; p : real; { локальные переменные }
begin m := n div 2 ; { целочисленное деление }
for i := 1 to m do
begin p := C[ i ]; C[i] := C[N-i+1]; C[N-i+1] := p end;
end.
6. Формирование массива из элементов другого массива, удовлетворяющих заданному условию
Задано: массив A = (a1, a2, ..., an), T - заданное число.
Сформировать: массив B = (b1, b2, ..., bn), состоящий из элементов массива, удовлетворяющих условию Ai > T.
Заметим, т.к. индексы элементов массивов A и B не совпадают (не все элементы массива Ai > T), то для обозначения индексов массива B должна быть предусмотрена другая переменная.
Исходные данные:
N - размер массива;
A - массив размером N;
T - заданное значение;
Результат:
B - массив размером не больше N;
Y - число элементов массива B;
Вспомогательная переменная: I - индекс - управляющая переменная цикла.
Procedure MAS_NEW (n:integer;T:real;A:mas;var B: mas; var Y: byte);
{ где mas должен быть описан в главной программе в разделе описания типов, например так :
type mas = array[1..100 ] of real ;
тогда это будет процедура для суммирования двух одномерных массивов размером не более 100 элементов }
{ процедура включения в новый массив элементов, удовлетворяющих условию }
begin Y := 0; { обнуление ячейки под счетчик элементов массива В }
for i := 1 to n do
If A[ i ] > T then begin Y := Y+1; B[ Y ] := A[ i ] end;
end.
7. Поиск максимального (минимального) элемента в массиве с запоминанием его положения в массиве.
Задано: массив A = (a1,a2,...,an).
Найти: max (min) элемент массива A и его индекс.
Исходные данные:
N - размер массива;
A - массив размером N;
Результат:
A_max - максимальный элемент массива A;
K - его индекс.
Вспомогательная переменная: I - индекс управляющая переменная цикла.
Procedure MAX_MAS1(n:integer; A :mas; var A_max :real; var K byte);
{ процедура поиска максимального элемента массива и его номера }
begin A_max := A[1]; K := 1;
for i := 2 to n do
If A_max<A[i] then begin K := i; A_max := A[i] end;
end.
Примечание: Если в массиве несколько max элементов (имеют одно и то же значение), то в K будет запоминаться первый из них, а чтобы запоминался индекс последнего нужно заменить условие на A_max<=A(I). Поиск минимального элемента аналогичная процедура.
8. Поиск заданного элемента в массиве
Задано: массив P=(p1,p2,...pn); элемент L (массив может быть как числовым так и символьным.
Найти: Есть ли в массиве P, элемент равный L. Результат присвоить символьной переменной.
Исходные данные:
N - размер массива;
P - массив размером N;
L - значение, которое ищется в массиве;
Результат: R - имеет значение "элемент, равный L есть" или "элемента, равного L нет" в зависимости от результата поиска;
Вспомогательная переменная: I - индекс управляющая переменная цикла.
Procedure POISK ( n:integer; P :mas; L :integer; var R :string);
{ процедура поиска заданного значения среди элементов массива }
Label m ;
begin
R :=" элемента равного L в массиве нет " ;
for i := 1 to n do
If P[i] = L then
begin R := " элемент, равный L есть "; Goto m end;
end.
Примечание. Если элемент, равный L, найден, то чтобы завершить цикл? используется оператор безусловного перехода Goto m, где локальная метка m обязательно должна быть описана в процедуре.
Алгоритмы поиска
Общая классификация алгоритмов поиска.
Все методы можно разделить на статические и динамические. При статическом поиске массив значений не меняется во время работы алгоритма. Во время динамического поиска массив может перестраиваться или изменять размерность. Рассмотрим поподробнее эти алгоритмы.
1. Алгоритм поиска по бинарному дереву.
Суть этого алгоритма достаточно проста. Представим себе, что у нас есть набор карточек с телефонными номерами и адресами людей. Карточки отсортированы в порядке возрастания телефонных номеров. Необходимо найти адрес человека, если мы знаем, что его номер телефона 222-22-22. Наши действия? Берем карточку из середины пачки, номер карточки 444-44-44. Сравнивая его с искомым номером, мы видим, что наш меньше и, значит, находится точно в первой половине пачки. Смело откладываем вторую часть пачки в сторону, она нам не нужна, массив поиска мы сузили ровно в два раза. Теперь берем карточку из середины оставшейся пачки, на ней номер 123-45-67. Из чего следует, что нужная нам карточка лежит во второй половине оставшейся пачки... Таким образом, при каждом сравнении, мы уменьшаем зону поиска в два раза. Отсюда и название метода - половинного деления или дихотомии.
Скорость сходимости этого алгоритма пропорциональна Log(2)N¹. Это означает, что не более, чем через Log(2)N сравнений, мы либо найдем нужное значение, либо убедимся в его отсутствии.
2. Поиск по "дереву Фибоначчи".
Трудноватый для восприятия метод, но эффективность его немного выше, чем у поиска по Бинарному дереву, хотя так же пропорциональна Log(2)N.
В дереве Фибоначчи числа в дочерних узлах отличаются от числа в родительском узле на одну и ту же величину, а именно на число Фибоначчи. Суть метода в том, что сравнивая наше искомое значение с очередным значением в массиве, мы не делим пополам новую зону поиска, как в бинарном поиске, а отступаем от предыдущего значения, с которым сравнивали, в нужную сторону на число Фибоначчи.
Почему этот способ считается более эффективным, чем предыдущий?
Дело в том, что метод Фибоначчи включает в себя только такие арифметические операции, как сложение и вычитание, нет необходимости в делении на 2, тем самым экономится процессорное время!
3. Метод экстраполяций.
Массив значений - это словарь, все значения в нем отсортированы по алфавиту. Искомое слово нам известно. Значит искать будем в отсортированном массиве.
Итак, искомое слово начинается на букву T, открываем словарь немного дальше, чем на середине. Нам попалась буква R, ясно, что искать надо во второй части словаря, а на сколько отступить? На половину? "Ну зачем же на половину, это больше, чем надо", скажете вы и будете правы. Ведь нам не просто известно, в какой части массива искомое значение, мы владеем еще и информацией о том, насколько далеко надо шагнуть!
Вот мы и подошли к сути рассматриваемого метода. В отличие от первых двух, он не просто определяет зону нового поиска, но и оценивает величину нового шага.
Алгоритм носит название экстраполяционного метода и имеет скорость сходимости большую, чем первые два метода.
Примечание:
Если при поиске по бинарному дереву за каждый шаг массив поиска уменьшался с N значений до N/2, то при этом методе за каждый шаг зона поиска уменьшается с N значений до корня квадратного из N. Если К лежит между Kn и Km, то следующий шаг делаем от n на величину
(n - m)*(K - Kn)/(Km - Kn)
Скорость экстраполяционнго метода начинает существенно превышать скорость метода половинного деления при больших значениях N.
Если необходимо искать в небольшом массиве и делать это нужно нечасто, проще воспользоваться методом перебора всех значений массива;
Если массив значений большой и искать нужно часто, необходимо отсортирорать массив и воспользовыаться методом половинного деления или интерполяционным методом. Каким из них именно, выбирать нужно исходя из того, насколько велик массив и какой метод легче реализовать в коде.
При предложенном выборе возникает резонный вопрос, а "большой массив" – это какой? При оценке времени, которое затрачивает алгоритм на поиск, имеют значение две величины. Во-первых, это размерность массива (количество элементов) и, во-вторых, это количество обращений (то есть сколько раз нам нужно в нем искать).
Итак, имеем массив размерностью N и проводим в нем поиск М раз.
Количество операций, которые выполнит алгоритм прямого перебора, пропорционально M * N. Метод дихотомии совершит 2М * Log(2)N операции, к тому же и время на сортировкку надо прибавить – N * Log(2)N.
Итак, имеем два выражения:
T1 = M*N;
T2 = 2М*Log(2)N + N*Log(2)N
При Т1 = Т2 мы находимся на границе, на которой одинаково оптимальны оба алгоритма. Из этого равенства можно получить области в системе координат "Количество обращений - Размерность массива".
Алгоритмы сортировки
Алгоритм 1. Сортировка вставками.
Это изящный и простой для понимания метод. Его суть состоит в том, что создается новый массив, в который мы последовательно вставляем элементы из исходного массива так, чтобы новый массив был упорядоченным. Вставка происходит следующим образом: в конце нового массива выделяется свободная ячейка, далее анализируется элемент, стоящий перед пустой ячейкой (если, конечно, пустая ячейка не стоит на первом месте), и если этот элемент больше вставляемого, то элемент подвигается в свободную ячейку (при этом на том месте, где он стоял, образуется пустая ячейка) и сравнивается следующий элемент. Так можно прийти к ситуации, когда элемент перед пустой ячейкой меньше вставляемого или пустая ячейка стоит в начале массива. Вставляемый элемент помещается в пустую ячейку. Таким образом, по очереди вставляются все элементы исходного массива. Очевидно, что если до вставки элемента массив был упорядочен, то после вставки перед вставленным элементом расположены все элементы, котрые меньше него, а после - больше. Так как порядок элементов в новом массиве не меняется, то сформированный массив будет упорядоченным после каждой вставки. А значит, после последней вставки получается упорядоченный исходный массив. Вот как такой алгоритм можно реализовать на языке программирования Pascal:
Program InsertionSort;
Var A,B : array[1..1000] of integer;
N,i,j : integer;
Begin
{Определение размера массива A (N) и его заполнение}
…
{сортировка данных}
for i:=1 to N do
begin
j:=i;
while (j>1) and (B[j-1]>A[i]) do
begin
B[j]:=B[j-1];
j:=j-1;
end;
B[j]:=A[i];
end;
{Вывод массива B}
…
End.
Алгоритм 2. Пузырьковая сортировка.
Реализация данного метода не требует дополнительной памяти. Метод очень прост и состоит в следующем: берется пара рядом стоящих элементов, и если элемент с меньшим индексом оказывается больше элемента с большим индексом, то они меняются их местами. Эти действия продолжаются, пока есть такие пары. Легко понять, что когда таких пар не останется, то данные будут отсортированными. Для упрощения поиска таких пар данные просматриваются по порядку от начала до конца. Из этого следует, что за такой просмотр находится максимум, который помещается в конец массива, а потому следующий раз достаточно просматривать уже меньшее количество элементов. Максимальный элемент как бы всплывает вверх, отсюда и название алгоритма. Так как каждый раз на свое место становится по крайней мере один элемент, то не потребуется более N проходов, где N - количество элементов. Вот как это можно реализовать:
Program BubbleSort;
Var A : array[1..1000] of integer;
N,i,j,p : integer;
Begin
{Определение размера массива A (N) и его заполнение}
…
{сортировка данных}
for i:=1 to n do
for j:=1 to n-i do
if A[j]>A[j+1] then
begin {Обмен элементов}
p:=A[j];
A[j]:=A[j+1];
A[j+1]:=P;
end;
{Вывод отсортированного массива A}
…
End.
Алгоритм 3. Сортировка Шейкером.
Когда данные сортируются не в оперативной памяти, а на жестком диске, особенно если ключ связан с большим объемом дополнительной информации, то количество перемещений элементов существенно влияет на время работы. Этот алгоритм уменьшает количество таких перемещений, действуя следующим образом: за один проход из всех элементов выбираются минимальный и максимальный. Потом минимальный элемент помещается в начало массива, а максимальный, соответственно, в конец. Далее алгоритм выполняется для остальных данных. Таким образом, за каждый проход два элемента помещаются на свои места, а значит, понадобится N/2 проходов, где N - количество элементов. Реализация данного алгоритма выглядит так:
Program ShakerSort;
Var A : array[1..1000] of integer;
N,i,j,p : integer;
Min, Max : integer;
Begin
{Определение размера массива A - N) и его заполнение}
…
{сортировка данных}
for i:=1 to n div 2 do
begin
if A[i]>A[i+1] then
begin
Min:=i+1;
Max:=i;
end
else
begin
Min:=i;
Max:=i+1;
end;
for j:=i+2 to n-i+1 do
if A[j]>A[Max] then
Max:=j
else
if A[j]<A[Min] then
Min:=j;
{Обмен элементов}
P:=A[i];
A[i]:=A[min];
A[min]:=P;
if max=i then
max:=min;
P:=A[N-i+1];
A[N-i+1]:=A[max];
A[max]:=P;
end;
{Вывод отсортированного массива A}
…
End.
Рассмотрев эти методы, сделаем определенные выводы. Их объединяет не только то, что они сортируют данные, но также и время их работы. В каждом из алгоритмов присутствуют вложенные циклы, время выполнения которых зависит от размера входных данных. Значит, общее время выполнения программ есть O(n2) (константа, умноженная на n2). Следует отметить, что первые два алгоритма используют также O(n2) перестановок, в то время как третий использует их O(n). Отсюда следует, что метод Шейкера является более выгодным для сортировки данных на внешних носителях информации.
Алгоритм 4. Сортировка слиянием.
Эта сортировка использует следующую подзадачу: есть два отсортированных массива, нужно сделать (слить) из них один отсортированный. Алгоритм сортировки работает по такому принципу: разбивается массив на две части, отсортировывается каждая из них, а потом сливаются обе части в одну отсортированную. Корректность данного метода практически очевидна, поэтому перейдем к реализации.
Program SlivSort;
Var A,B : array[1..1000] of integer;
N : integer;
Procedure Sliv(p,q : integer); {процедура сливающая массивы}
Var r,i,j,k : integer;
Begin
r:=(p+q) div 2;
i:=p;
j:=r+1;
for k:=p to q do
if (i<=r) and ((j>q) or (a[i]<a[j])) then
begin
b[k]:=a[i];
i:=i+1;
end
else
begin
b[k]:=a[j];
j:=j+1;
end ;
for k:=p to q do
a[k]:=b[k];
End;
Procedure Sort(p,q : integer); {p,q - индексы начала и конца сортируемой части массива}
Begin
if p<q then {массив из одного элемента тривиально упорядочен}
begin
Sort(p,(p+q) div 2);
Sort((p+q) div 2 + 1,q);
Sliv(p,q);
end;
End;
Begin
{Определение размера массива A - N) и его заполнение}
…
{запуск сортирующей процедуры}
Sort(1,N);
{Вывод отсортированного массива A}
…
End.
Чтобы оценить время работы этого алгоритма, составим рекуррентное соотношение. Пускай T(n) - время сортировки массива длины n, тогда для сортировки слиянием справедливо T(n)=2T(n/2)+O(n) (O(n) - это время, необходимое на то, чтобы слить два массива). Распишем это соотношение:
T(n) = 2T(n/2) + O(n) = 4T(n/4) + 2O(n/2) + O(n) = 4T(n/4) + 2O(n) = … = 2kT(1) + kO(n)
Осталось оценить k. Мы знаем, что 2k = n, а значит k = log2n. Уравнение примет вид T(n) = nT(1) + log2nO(n). Так как T(1) - константа, то T(n) = O(n) + log2nO(n) = O(nlog2n). То есть, оценка времени работы сортировки слиянием меньше, чем у первых трех алгоритмов.
| < Предыдущая | Следующая > |
|---|







