25.08.2014 19:36
Александр
Математическая логика имеет непосредственную связь с теорией проектирования ЭВМ. С помощью логических функций и законов математической логики может быть описано поведение различных компонентов ЭВМ. Кроме того, современные языки программирования немыслимы без встроенных в них логических функций.
При записи тех или иных логических выражений используется специальный язык, который принят в математической логике. Ее основоположником является великий немецкий математик Готфрид Вильгельм Лейбниц. Ирландский математик Джордж Буль продолжил создание математической логики, которая оперирует не числами, а высказываниями. Высказывание - это любое утверждение, относительно которого можно сказать: истинно оно или ложно.
Так, например, предложение “7 - нечетное число” следует считать высказыванием, так как оно истинное. Предложение “Июль - зимний месяц” тоже высказывание, так как оно ложное.
Разумеется, не всякое предложение является логическим высказыванием. Высказываниями не являются, например, предложения “ученик десятого класса” и “информатика - интересный предмет”. Первое предложение ничего не утверждает об ученике, а второе использует слишком неопределённое понятие “интересный предмет”. Вопросительные и восклицательные предложения также не являются высказываниями, поскольку говорить об их истинности или ложности не имеет смысла.
Предложения типа “в городе A более миллиона жителей”, “у него голубые глаза” не являются высказываниями, так как для выяснения их истинности или ложности нужны дополнительные сведения: о каком конкретно городе или человеке идет речь. Такие предложения называются высказывательными формами.
Подробнее...
25.08.2014 19:01
Александр
Прежде чем определить понятие конечного графа в наиболее общей форме, представим себе на плоскости (или в вещественном аффинном пространстве произвольной размерности k) некоторое конечное множество V точек и конечный набор Х линий, соединяющих некоторые пары точек из V. Указанной геометрической конфигурацией описывается, например, схема автомобильных дорог, связывающих города некоторой области (рисунок 3).
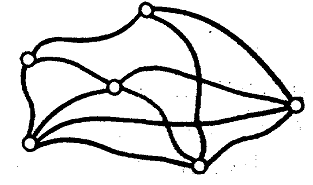
Рисунок 3 – Пример схемы автодорог
Подробнее...
25.08.2014 18:43
Александр
В отличие от аналоговых электронных устройств, в цифровых устройствах (ЦУ) входные и выходные сигналы могут принимать ограниченное количество состояний. В соответствии с логическим соглашением (ГОСТ 2.743-82), в зависимости от конкретной физической реализации элементов ЦУ, более положительному значению физической величины, "H" - уровень, соответствует состояние "логическая 1", а менее положительному значению,"L - уровень" - "логический 0". Такое соглашение называется положительной логикой. Обратное соотношение называется отрицательной логикой. В ГОСТе 19480 - 89 даны наименования, определения и условные обозначения основных параметров и характеристик цифровых микросхем.
Теоретической основой проектирования ЦУ является алгебра-логики или булева алгебра, оперирующая логическими переменными. Для логических переменных, принимающих только два значения, существуют 4 основных операции. Операция логическое "И" (AND) конъюнкция или логическое умножение, обозначается * или /\. Операция логическое "ИЛИ" (OR), дизъюнкция или логическое сложение, обозначается + или \/. Операция логическое "НЕ" (NOT), изменение значения, инверсия или отрицание, обозначается чертой над логическим выражением. Инверсия иногда будет в тексте обозначаться знаком "~". Операция эквивалентности обозначается "=".
Подробнее...
25.08.2014 16:44
Александр
Общие понятия систем счисления
Способ представления чисел посредством числовых знаков (цифр) называется системой счисления (СС). Правила записи и действий над числами в системах счисления, используемых в цифровой вычислительной технике, определяют арифметические основы цифровых ЭВМ.
Различают два основных вида систем счисления: непозиционные и позиционные.
Непозиционные системы счисления характеризуются тем, что значение числа, выражаемое совокупностью цифр, определяется только конфигурацией цифровых символов. Классическим примером непозиционной системы является римская система счисления.
Наибольшее распространение получили позиционные системы счисления, в которых значение любой цифры определяется не только конфигурацией ее символа, но и местоположением (позицией), которое она занимает в числе. При этом под основанием позиционной системы счисления q понимается количество различных цифр, используемых для представления числа.
Подробнее...
25.08.2014 16:43
Александр
В ЭВМ применяется двоичная система счисления, т.е. все числа в компьютере представляются с помощью нулей и единиц, поэтому компьютер может обрабатывать только информацию, представленную в цифровой форме.
Для преобразования числовой, текстовой, графической, звуковой информации в цифровую необходимо применить кодирование.
Кодирование – это преобразование данных одного типа через данные другого типа. В ЭВМ применяется система двоичного кодирования, основанная на представлении данных последовательностью двух знаков: 1 и 0, которые называются двоичными цифрами (binary digit – сокращенно bit).
Целые числа кодируются двоичным кодом довольно просто (путем деления числа на два). Для кодирования нечисловой информации используется следующий алгоритм: все возможные значения кодируемой информации нумеруются и эти номера кодируются с помощью двоичного кода.
Подробнее...
25.08.2014 16:30
Александр
Количественные характеристики информации
Классификация мер информации представлена на рис.1.

Рис. 1. Классификация мер информации
Подробнее...
25.08.2014 16:27
Александр
Прежде всего, следует определиться с тем, что следует понимать под термином - «информатика"? В понимании некоторых людей – это совокупность приемов и методов работы с компьютером. На самом деле, ПК является лишь техническим средством, с помощью которого Информатика реализует свой прикладной пользовательский аспект.
Накопленный объем теоретических и практических знаний в современной информатике очень велик и при этом динамичен. Однако, из какого бы определения не исходить, у современной информатики есть два взаимодополняющих аспекта – научный и технологический. Первый является более устоявшимся, второй – весьма мобильный. Главное при изучении информатики – освоить фундаментальные понятия каждой из ее областей, ориентироваться в их взаимосвязи, приобрести навыки практической работы с важнейшими техническими и программными средствами
Термин "информатика" (франц. informatique) происходит от французских словinformation (информация) и automatique (автоматика) и дословно означает"информационная автоматика".
Широко распространён также англоязычный вариант этого термина - "Сomputer science", что означает буквально "компьютерная наука".
Информатика - это основанная на использовании компьютерной техники дисциплина, изучающая структуру и общие свойства информации, а также закономерности и методы её создания, хранения, поиска, преобразования, передачи и применения в различных сферах человеческой деятельности.
Подробнее...
25.08.2014 16:20
Александр
Понятие информатики является относительно новым в лексиконе современного человека. Несмотря на повсеместное употребление, его содержание остается не проясненным до конца в силу своей новизны. Вследствие широкого распространения компьютеров и информационного бума, который переживает человечество, с азами информатики должен быть знаком всякий грамотный современный человек; вот почему ее преподавание в высшей школе исключительно важно.
Информатика – область человеческой деятельности, связанная с процессами преобразования информации с помощью компьютеров и других средств вычислительной техники. С информатикой часто связывают одно из следующих понятий: это либо совокупность определенных средств преобразования информации, либо фундаментальная наука, либо отрасль производства, либо прикладная дисциплина.
Подробнее...
|
|









